How Audacia implements Google OR-Tools into software development projects

The vast majority of business problems relate to minimising costs. With many possible solutions available, the ‘best’ option could be defined as the one which maximises one of these desired outcomes . How we evaluate these solutions is often based on a preconceived notion about characteristics that make them ‘good’. But what if you don't know how you would have come to that solution, and how do you know which solution is 'best'? The objective of using Google OR-Tools is to find a solution to your problem based on the parameters that you define. This can either be to find the single ‘best’ solution or to find a feasible solution that does not violate any of your defined constraints. In this article, we will implement a simple optimisation model using Google OR-Tools by solving a classic Vehicle Routing Problem (VRP).

Not knowing the 'how'

The main challenge in implementing a successful business process model is reducing a business problem into rules (or constraints). If you can represent a problem with a list of criteria that must be met, you are 90% of the way there in terms of being able to solve that problem - the key area of focus can be on the what, rather than the how.

Use cases

As mentioned earlier, a large proportion of modern business problems can be presented as optimisation problems, such as:

• Assigning repair people to customers requiring home visits, ensuring all customers are visited in a specific time period.
• Loading a fleet of vehicles with products minimising the number of vehicles needed.
• Creating a weekly schedule of shifts for a workforce ensuring their minimum weekly hours are met.

Examples like these are well documented on the Google OR-Tools website.

Feasible vs optimal

Not all problems require a perfect solution. In most cases, merely finding a more efficient solution is enough. A good real-world example of this is scheduling shifts for employees.

Shift scheduling can quite easily turn into an optimisation problem when you start taking into account preferences. For example:

• Employee A would prefer not to work on weekends.
• Ideally, at least 2 people would work on a Friday.

In OR-Tools, words like 'ideally' and 'prefer' translate into what we call a soft constraint. By soft constraint we mean that if these criteria were not to be met, it wouldn't be a deal-breaker, especially if it were the only feasible solution. Models which take into account these preferences will score a solution based on how many times this criterion was (or was not) met.

A feasible solution is one such that all hard (or mandatory ) constraints have been met. This solution becomes optimal when the score of a solution is better than all other feasible solutions. In contrast to soft constraints, a hard constraint for this kind of problem could be any of the following:

• Employee B cannot work on Tuesday evenings.
• No more than 4 people can work at the same time.

About OR-Tools

OR-Tools is Google's award-winning suite of tools which allow a developer to solve problems using combinatorial optimisation. One of its primary functions is to provide an easy-to-use model building API as a wrapper around industry-recognised solvers. Rather than siding with a "one solver fits all" approach, developers have the option to specify which solver to use (should they have a preference) or to let the software choose the most appropriate.

The Google OR-Tools project is open source and Audacia have even helped to contribute to it (here).

The solvers implemented by OR-Tools range from commercial (e.g. IBM's CPLEX solver) to open source (e.g. SCIP). Google has also written its own award-winning CP-SAT solver for solving constraint programming problems.

The Google OR-Tools website, source code, and forums are littered with examples of real-world problem-solving. As a result, it does not usually take long to find an existing use-case similar to your own.

OR-Tools can be implemented in projects written in Python, Java, C++, and most importantly for us, .NET. This flexibility allows .NET developers to write models in C# as opposed to similar software packages like OptaPlanner (Java) and GECODE (C++).

Using OR-Tools in .NET

Google OR-Tools can be used in a .NET project via a NuGet package. The package automatically adds a DLL reference to your project. Depending on your operating system, you will also need to add a reference to the Windows/OSX/Linux runtime.

Worked example - Assigning repair people

This is a Vehicle Routing Problem (VRP), not dissimilar to a Travelling Salesman Problem (TSP), which you may have come across if you have spent any time with optimisation problems.

Suppose we are a company that fixes laptops via home visits. Each day, this company has a list of customers to visit and must therefore assign employees (the repair people) to each customer. We would like to minimise the distance travelled by the employees so that they are reducing the amount of fuel to expense and are spending less time on the road as a result. As you can imagine, finding an optimal solution for this problem could save a lot of money on a daily basis.

Once we have a working example of assigning our repair people, we will introduce time windows to demonstrate how to incorporate real-life constraints into a problem like this.

First, consider a graph with the customer locations as the nodes and the distance between each customer as the edges. In graph theory, this is referred to as a complete graph. A complete graph with n nodes is referred to as K_n. Below is an example of how we can represent a K₄ graph as a matrix.

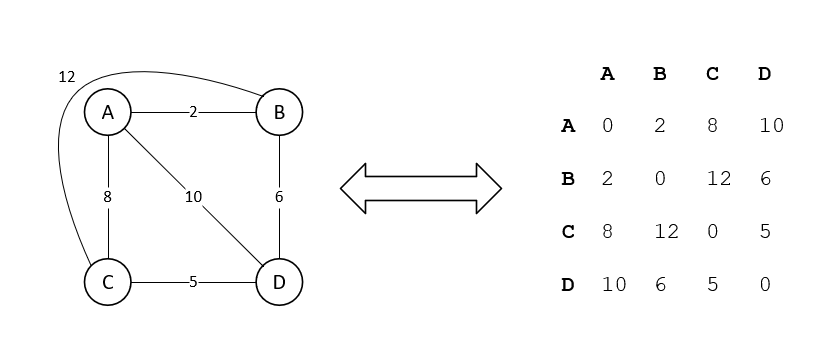
NB this example is undirected i.e i => j == j => i for all i,j (in other words, the matrix is symmetric). This may not be the case in real-life scenarios.

In graph theory, this problem is equivalent to finding the Hamiltonian Path (i.e. a path visiting each node exactly once) of minimum weight.

Step 1: Distance matrix

The first step is to create an n x n matrix where matrix[i,j] returns the distance between point i and j.

var distances = new long[,] {
    { 0, 2, 8, 10 },
    { 2, 0, 12, 6 },
    { 8, 12, 0, 5 }.
    { 10, 6, 5, 0 }
};

The data is represented in a matrix so that we can quickly determine the pre-calculated distance between two locations. This helps to keep our distance callback logic clear and concise. The distance between two locations can either be a simple Euclidean distance (i.e. as the crow flies), or something more complicated; perhaps using a routing API like google itself.

Step 2: Create the index manager

A lot of variables are added when creating a model and adding constraints. Each location (node) has both a nodeIndex and a variableIndex. Only the variableIndex's are used for solving, whereas the nodeIndex's are used so that we know which locations have been chosen.

Concretely, 1. We add locations as nodes, creating the nodeIndex's. 1. The solver registers each node and creates variables representing them (the variableIndex's). 1. The solver uses the variableIndex's to create a solution, returning an ordered list of the variableIndex's. 1. We ask the RoutingIndexManager what nodeIndex's these variableIndex's represent.

The RoutingIndexManger is set up as below:

int numberOfLocations = 4;
int numberOfVehicles = 1;
int startingNode = 0;
var indexManager = new RoutingIndexManager(
    numberOfLocations, // Our location count, including depot (A) 
    numberOfVehicles, // The number of repair people
    startingNode // The index of the depot (0 for A, 1 for B, etc.)
);

The two main uses of the RoutingIndexManager are: - NodeToIndex - Get the variableIndex from a given nodeIndex. - IndexToNode- Get the nodeIndex from a given variableIndex.

Once solved, we can use the IndexToNode method to infer the selected locations from the solution.

Once we have this RoutingIndexManager, we can create our RoutingModel:

var routing = new RoutingModel(manager);

An instance of this class contains all information required to find a solution. Later on, we'll call routing.SolveWithParameters(...) to obtain a solution.

Step 3: Distance callback

We can now make use of our distance matrix. For the model to find a solution to the problem, it will need to continually refer back to something to tell it the distance between two nodes. This takes two steps:

  Func<long, long, long> distanceFunc = (fromVariableIndex, toVariableIndex) = {
     // Get the node indexes from the variable indexes;
    long fromNodeIndex = manager.IndexToNode(fromVariableIndex);
    long toNodeIndex = manager.IndexToNode(toVariableIndex);
    return matrix[fromNodeIndex, toNodeIndex];

  int distanceCallbackIndex = routing.RegisterTransitCallback(
      distanceFunc // A func to evaluate the weight between two nodes
  );

1. Register a callback for the model to look up when checking two nodes:

The solver registers this transit callback, and returns an index (distanceCallbackIndex) which serves as this callback's unique identifier. Registering this callback tells the model to run this Func each time it is deciding which node to select next. If more callbacks are registered (e.g. if we were to keep track of travel time also), we would call this method again, returning a different index.

2. Tell the model that this index should be used as the weight of the path (or arc) between two nodes.

   routing.SetArcCostEvaluatorOfAllVehicles(distanceCallbackIndex);

You may be wondering why the model does not automatically use the index created in step one as the distance. You can specify many indexes for the model to keep tabs on as it is calculating. This enables you to keep running totals of whatever you like (e.g. the distance a specific vehicle has travelled or travel time for all vehicles).

The matrix was set up to make this distance callback as simple as possible. You have the power to make the 'distance' between two nodes anything you like, but be aware that performance can suffer drastically should you introduce anything particularly computation-heavy within a callback.

Step 4: Travel time callback

Similarly to step 3, we can create a timeFunc. This behaves just like distanceFunc, but returns the time it takes to travel between two locations.

Once we've registered this timeFunc as a transit callback (and returned a timeCallbackIndex), we create a dimension to keep track of a running time total:

routing.AddDimension(
    timeCallbackIndex, // transit callback
    20,                // slack
    10000,             // max capacity
    false,             // start cumul to zero
    "Time"             // dimension name
); 

• timeCallbackIndex: this code was omitted for brevity, but was created in the same way as the distanceCallbackIndex, using the timeFunc.
• slack: This slack variable gives the model some wiggle-room, and allows for a maximum of 20 minutes delay per location. For example, the repair man doing work before/after the visit, the customer not answering the door initially etc. This is a great example of Google OR-Tools’ flexibility when it comes to solving real-life problems.
• max capacity: This represents the maximum time taken. In some cases, you can calculate exactly what this maximum should be. However, in most cases, it is easier to set it to an arbitrarily large number, provided you are sure the time can never exceed this value. The max time taken is not particularly relevant in this scenario but remains very important for keeping track of vehicle capacities (i.e. you are performing collections and a vehicle can only fit so much inside).
• start cumul to zero: This represents whether time should be relative to each vehicle's starting time or not. This is not relevant in our current scenario as both drivers will be leaving immediately and won't be returning to site until all tasks are done. This can be set to true, but it would be advised that you limit the distance a vehicle travels to a single outing, rather than as a whole.
• dimension name: An identifier for this dimension, so we can get it back from the routing model.

We can now access the dimension, and the cumulative totals it is keeping track of.

RoutingDimension timeDimension = routing.GetMutableDimension("Time");

// for each visit, we can get the variables representing snapshot information at that visit
for (var nodeIndex = 0; nodeIndex < numberOfLocations; nodeIndex++) 
{
    long variableIndex = manager.NodeToIndex(nodeIndex);
    IntVar slackAtLocation = timeDimension.SlackVar(variableIndex);
    IntVar travelTimeToLocation = timeDimension.TransitVar(variableIndex);
    IntVar totalTimeTaken = timeDimension.CumulVar(variableIndex);
}

• slackAtLocation: how much time is spent waiting at this visit (as above, this is a number between 0 and 20).
• travelTimeToLocation: how long it took the driver to get to this location (i.e the value returned by the timeFunc for this and the previous node).
• totalTimeTaken: how much time has elapsed since the driver left the depot. This is key for creating constraints.

IntVar

This is a Google OR-Tools object , wrapping an integer value, which represents the solution provided to us by the model. Once we have a solution, you can use solution.Value(intVar) to get the value of that specific variable, if necessary.

Step 5: Add deadline constraints

As posed by this problem, we have a time window in which to complete each visit. What this means in the code is that each location has a min & max time it needs to be visited by.

Slack is very useful here as it allows the driver to wait at a location before setting off to the next location. You can think of slack as 'padding' to help meet things like time window constraints. The slack at a location is included in its cumulative time; some pseudo-code: CumulVar(i) = CumulVar(i-1) + Slack(i) + Transit(i-1, i).

For time window constraints, the upper and lower bounds are added as follows:

timeDimension.CumulVar(variableIndex).SetRange(minTime, maxTime);

Penalties

Rather than enforcing hard constraints, you have the option to set a penalty for lateness. Implementing penalties correctly is a good way to control the behaviour of your model. We can do this by replacing the SetRange code in step 5 with the below:

// with this
const int penalty = 1000; // The higher this number, the worse it is in a minimization problem
timeDimension.SetCumulVarLowerBound(variableIndex, startWindow, penalty);
timeDimension.SetCumulVarUpperBound(variableIndex, endWindow, penalty);

The effect this has is that, rather than this not being a feasible solution, this solution is outputted with the penalty included in the score of the objectiveValue.

Step 6: Solve

At this stage we have a 'complete' model, we can solve. To do this, the routing model requires search parameters with the PathCheapestArc strategy ensuring it minimizes the distance travelled by all vehicles. The Google OR-Tools class operations_research_constraint_solver exposes default search parameters for us to use.

// Use Google's default search parameters.
SearchParameters searchParameters = operations_research_constraint_solver.DefaultRoutingSearchParameters();

// Minimize the total distance the vehicle travels to visit all customers.
searchParameters.FirstSolutionStrategy = FirstSolutionStrategy.Types.Value.PathCheapestArc;

Assignment solution = routing.SolveWithParameters(searchParameters);

// This is the length of the shortest path/arc, plus any penalties incurred.
long objectiveValue = solution.ObjectiveValue();

These search parameters can become a lot more sophisticated. Based on your requirements, you can for example: - Set a solution limit, to exit when a certain number of feasible solutions have been found. - Set a time limit, to exit out after a certain period of time. See the routing options for the full list of parameters.

Using the solution we created, and the original RoutingModel , we can obtain the selected locations as follows:

long currentVariableIndex = routing.Start(0);
var locationNumber = 0;
Console.WriteLine($"Objective value: {solution.ObjectiveValue()}");
// Now we've solved, the routing model knows when we've ended or not
while (!routing.IsEnd(index))
{
    // Get the next selected location
    currentVariableIndex = solution.Value(routing.NextVar(currentVariableIndex));
    var nodeIndex = routingIndexManager.IndexToNode((int)index);
    Console.WriteLine($"Location number {locationNumber}: {nodeIndex}");
}

Case 1: without time windows:

When no time windows are applied, we will obtain a solution that gives us the shortest path. This path is A -> B -> D -> C:

Objective value: 13
Location number 1: 0
Location number 2: 1
Location number 3: 3
Location number 4: 2

Case 2: with time windows:

If we were to add a time window, such that location C must be visited between 0 and 10 (I have deliberately left out the units here but you can think of this as minutes or hours if that helps)our previous example would no longer work, as location C is visited at 13. Using the code in step 5, we are provided with the path A -> C -> D -> B. While this has a lower objective value, it visits C first and therefore the constraint is met.

Objective value: 19
Location number 1: 0
Location number 2: 2
Location number 3: 3
Location number 4: 1

Potential enhancements

It is possible to make this model more sophisticated by introducing new rules such as: - Customer A must be visited between 11:00-12:00. - Vehicle B must travel no more than 100 miles. - Vehicle C can visit no more than 5 customers.

Unit testing

Due to not having control over how a solution is found, the need for ensuring your model is well tested is vital. As mentioned above, the ability to break a problem down into a list of constraints can be used as inspiration for some test cases. Let’s take this time window as an example for a test case:

[Fact]
public void Visit_is_not_scheduled_before_the_start_of_a_customers_time_window()
{
    // For brevity, these parameters have everything the model needs to 
    // solve i.e distance matrix, time windows, number of vehicles, etc.
    var parameters = GetParameters();
    // Set the time window for customer A in the format [min,max]
    parameters.TimeWindows[0] = [100, 200];

    var result = _repairManScheduler.Execute(parameters);

    var visitedCustomer = GetVisitForCustomerAtIndex(result, 0);
    visitedCustomer.StartTime.Should().BeGreaterThanOrEqualTo(100);
}

Here, we have done the following: - Defined a constraint via the method name. - Set up the test data (in this case by creating a visit and specifying a time window). - Invoked the solver, passing in our test data. - Ensured the result has scheduled the visit to take place after the customer’s minimum time.

These problems are usually hard to test in terms of the data setup required and the time taken to inspect results. However, having unit tests to cover the fundamental constraints of your model is a great foundation to minimize regression issues further down the line, especially if the model is becoming more complex as time goes on.

Conclusion

We have shown that in a short amount of time we can implement a solution to the Vehicle Routing Problem with Time Windows (VRPTW) problem using Google OR-Tools. In real life uses, these models are generally more complex and built completely bespoke to a client's requirements. Audacia have now successfully implemented Google OR-Tools on a number of projects with models ranging from task scheduling to capacity planning.