In part two of our OR-Tools series, we showed how to solve a scheduling problem using OR-Tools. The third and final instalment of this series concerns an assignment problem - handing out pizzas to employees. Put differently, each pizza must be assigned to an employee and optimise how much they like their pizza in the process.
3. Assigning
As with previous stages, we have several rules that will condition the execution:
Each employee is given a maximum of one pizza Each pizza is distributed once (you can’t share a pizza!) Pizzas are leftover if there are more pizzas than employees
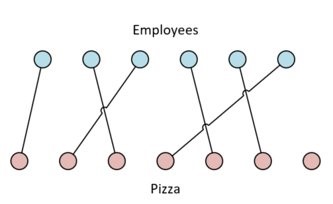
Here we have a bipartite graph with many-to-many correspondences. This graph is showing us that, while we can have a leftover pizza, every employee must be assigned a pizza first.
3.1. Unit Tests
The first test is Each_employee_gets_a_pizza() (below). The test is not specifying preference at this point. All we are concerned with is that the dictionary returns a count of employees; so, it has X amount items in it, where X is the number of employees, regardless of their assigned pizza type.
[Fact]
public void Each_employee_gets_a_pizza()
{
var random = new System.Random();
var employees = new List
{
new(random.Forename(), random.Next(0, 10), random.Next(0, 10), random.Next(0, 10)),
new(random.Forename(), random.Next(0, 10), random.Next(0, 10), random.Next(0, 10)),
new(random.Forename(), random.Next(0, 10), random.Next(0, 10), random.Next(0, 10))
};
var model = new AssignPizzaModel
{
Employees = employees,
// Make more than enough pizzas
Pizzas = Enumerable.Range(0, 10)
.Select(_ => random.Enum())
.ToList()
};
var solver = new AssignPizzaSolver(model);
var assignment = solver.Solve();
assignment.Should().HaveCount(employees.Count);
}
Moving on, Undesirable_pizzas_are_left_over() is for when we have a surplus of pizzas, and employees do not like one type of pizza as much as the other.
[Fact]
public void Undesirable_pizzas_are_left_over()
{
// Create some employees that all don't like hawaiian as much as the other types
var random = new System.Random();
var employees = new List
{
new(random.Forename(), margheritaPreference: 10, pepperoniPreference: 10, hawaiianPreference: 9),
new(random.Forename(), margheritaPreference: 10, pepperoniPreference: 10, hawaiianPreference: 9)
};
var model = new AssignPizzaModel
{
Employees = employees,
Pizzas = new List {PizzaType.Margherita, PizzaType.Pepperoni, PizzaType.Hawaiian}
};
var solver = new AssignPizzaSolver(model);
var assignment = solver.Solve();
assignment.Values.Should().NotContain(PizzaType.Hawaiian);
}
As we’re still making every type of pizza, what we are stating here is that the values do not contain the undesirable pizza type. In this case, we see that Hawaiian has been specified as the undesirable type, which means that one employee would receive margherita, one would receive pepperoni and the Hawaiian would be leftover.
[Fact]
public void Assigns_pizzas_that_people_like_the_most()
{
var random = new System.Random();
var firstPerson = random.Forename();
var secondPerson = random.Forename();
var thirdPerson = random.Forename();
var employees = new List
{
new(firstPerson, margheritaPreference: 6, pepperoniPreference: 2, hawaiianPreference: 2),
new(secondPerson, margheritaPreference: 10, pepperoniPreference: 8, hawaiianPreference: 7),
new(thirdPerson, margheritaPreference: 10, pepperoniPreference: 9, hawaiianPreference: 2)
};
var model = new AssignPizzaModel
{
Employees = employees,
Pizzas = new List {PizzaType.Margherita, PizzaType.Pepperoni, PizzaType.Hawaiian}
};
var solver = new AssignPizzaSolver(model);
var assignment = solver.Solve();
// Though the first person isn't as passionate about margherita as the rest, they really don't like the others
assignment[firstPerson].Should().Be(PizzaType.Margherita);
assignment[secondPerson].Should().Be(PizzaType.Hawaiian);
assignment[thirdPerson].Should().Be(PizzaType.Pepperoni);
}
Our third and final test looks at how best to optimise the satisfaction of employees through the pizzas they receive. In our example here, we can see that the first employee likes margherita (with a score of 6) not as much as his colleagues, but really dislikes pepperoni (which is scored at 2).
The model adds up the scores of the pizzas that people like and the only way to get 22 - the highest score and optimal solution - is by assigning pizzas that contribute to the higher score. On this basis, the first employee should get a margherita pizza even if they do not like it as much as everyone else.
3.2. Assign Pizza Solver Explained
var model = new CpModel();
IntVar[,] costVars = new IntVar[_numEmployees, _numPizzas];
IntVar[] flattenedCostVars = new IntVar[_numEmployees * _numPizzas];
int[] flattenedCosts = new int[_numEmployees * _numPizzas];
SetModelVars(costVars, model, flattenedCostVars, flattenedCosts);
AddConstraints(costVars, model);
// set the objective of the model
model.Maximize(LinearExpr.ScalProd(flattenedCostVars, flattenedCosts));
// Solve
CpSolver solver = new ();
var status = solver.Solve(model);
if (status != CpSolverStatus.Optimal)
{
throw OptimisationException.SubOptimalCpSolution(status);
}
If we recall our 2x2 matrix, the costVars is a two-dimensional matrix of 0s and 1s, which refers to whether employees have a pizza or not - if it's a 0 they do not have a pizza, if it is a 1 then they do.
For each costVars, we create a flattenedCostVars, which can be thought of as a flattened matrix or a long list of 0s and 1s. This is how much every employee likes pizza, formatted as one long list.
In terms of the objective of the model; we are multiplying a list of 1s and 0s with a list of how much each employee likes every pizza. So, the scale product of the flattenedCostVars - which are the variables that the model is deciding to set to 1 or 0 with the known list of costs is our score that we are trying to maximise.
for (var employeeIndex = 0; employeeIndex < _numEmployees; ++employeeIndex)
{
for (var pizzaIndex = 0; pizzaIndex < _numPizzas; ++pizzaIndex)
{
// create a variable that is set to 1 if this employee is given this pizza, and 0 otherwise
costVars[employeeIndex, pizzaIndex] = model.NewIntVar(0, 1, $"employee_{employeeIndex}_pizza_{pizzaIndex}");
var flattenedIndex = employeeIndex * _numPizzas + pizzaIndex;
flattenedCostVars[flattenedIndex] = costVars[employeeIndex, pizzaIndex];
flattenedCosts[flattenedIndex] = _costs[employeeIndex, pizzaIndex];
}
}
We set the model.NewIntVar and, for each employee and for each pizza, we declare a variable between 0 and 1. This is then set on the array and the constraints are added.
private void AddConstraints(IntVar[,] costVars, CpModel model)
{
// Ensure one pizza per employee
for (var employeeIndex = 0; employeeIndex < _numEmployees; employeeIndex++)
{
IntVar[] assignments = new IntVar[_numPizzas];
for (var pizzaIndex = 0; pizzaIndex < _numPizzas; pizzaIndex++)
{
assignments[pizzaIndex] = costVars[employeeIndex, pizzaIndex];
}
model.Add(LinearExpr.Sum(assignments) == 1);
}
// Ensure no pizza is given out more than once
for (var pizzaIndex = 0; pizzaIndex < _numPizzas; ++pizzaIndex)
{
IntVar[] vars = new IntVar[_numEmployees];
for (var employeeIndex = 0; employeeIndex < _numEmployees; ++employeeIndex)
{
vars[employeeIndex] = costVars[employeeIndex, pizzaIndex];
}
model.Add(LinearExpr.Sum(vars) <= 1);
}
}
We then add the constraints which are that, for each employee, we have in the costVars and we say that the assignments is a list of all the pizzas that employees could have. The sum of the array must equal 1, to ensure that each employee gets no more or less than their one allocated pizza.
And then we say to ensure that no pizza is given out more than once. This function is like the constraint that follows it, but with the exception that this is less than or equal to. This is so that if there are more employees than pizza, the model will not give out the worst pizza.
Final Statements This is a very dense example, which can feel particularly complex upon first viewing. Should you wish to revisit the case study, or try it out for yourself, you can access the code samples by cloning our OrToolsPlayground repo here. You can also find the Audacia.Random repo under the same organisation.
OR-Tools repo is also available; this is the source code for Google OR-Tools and will showcase some more examples, some of which Audacia has contributed to. For a variety of examples in different languages, look to the OR-Tools homepage.
This piece was originally delivered as a lecture for the Leeds Digital Festival.
Audacia is a software development company based in the UK, headquartered in Leeds. View more technical insights from our teams of consultants, business analysts, developers and testers on our technology insights blog.
Technology Insights

